RELACIÓN O TABLA
tabla en las bases de datos, se refiere al tipo de modelado de datos, donde se guardan y almacenan los datos recogidos por un programa. Su estructura general se asemeja a la vista general de un programa de hoja de cálculo.
Una tabla es utilizada para organizar y presentar información. Las tablas se componen de filas y columnas de celdas que se pueden rellenar con textos y gráficos.
Las tablas se componen de dos estructuras:
- Registro: es cada una de las filas en que se divide la tabla. Cada registro contiene datos de los mismos tipos que los demás registros. Ejemplo: en una tabla de nombre
- RELACIÓN O TABLAtabla en las bases de datos, se refiere al tipo de modelado de datos, donde se guardan y almacenan los datos recogidos por un programa. Su estructura general se asemeja a la vista general de un programa de hoja de cálculo.Una tabla es utilizada para organizar y presentar información. Las tablas se componen de filas y columnas de celdas que se pueden rellenar con textos y gráficos.Las tablas se componen de dos estructuras:
- Registro: es cada una de las filas en que se divide la tabla. Cada registro contiene datos de los mismos tipos que los demás registros. Ejemplo: en una tabla de nombres ,direcciones, etc, cada fila contendrá un nombre y una dirección.
- Campo: es cada una de las columnas que forman la tabla. Contienen datos de tipo diferente a los de otros campos. En el ejemplo anterior, un campo contendrá un tipo de datos único, como una dirección, o un número de teléfono, un nombre, etc.
A los campos se les puede asignar, además, propiedades especiales que afectan a los registros insertados. El campo puede ser definido como índice o autoincrementable, lo cual permiteBASE DE DATOS que los datos de ese campo cambien solos o sean el principal a la hora de ordenar los datos contenidos.
Cada tabla creada debe tener un nombre único en la Base de Datos, haciéndola accesible mediante su nombre o su seudónimo (Alias) (dependiendo del tipo de base de datos elegida). La estructura de las tablas viene dada por la forma de un archivo plano, los cuales en un inicio se componían de un modo similar.
BASES DE DATOS
1: Una base de datos es un “almacén” que nos permite guardar grandes cantidades de información de forma organizada para que luego podamos encontrar y utilizar fácilmente. A continuación te presentamos una guía que te explicará el concepto y características de las bases de datos.
2:Una base de datos es un conjunto de datos pertenecientes a un mismo contexto y almacenados sistemáticamente para su posterior uso. En este sentido; una biblioteca puede considerarse una base de datos compuesta en su mayoría por documentos y textos impresos en papel e indexados para su consulta. Actualmente, y debido al desarrollo tecnológico de campos como la informática y la electrónica, la mayoría de las bases de datos están en formato digital, siendo este un componente electrónico, por tanto se ha desarrollado y se ofrece un amplio rango de soluciones al problema del almacenamiento de datos.
3: los sistemas gestores de bases de datos son la herramienta más adecuada para almacenar los datos en un sistema de información debido a sus características de seguridad, recuperación ante fallos, gestión centralizada, estandarización del lenguaje de consulta y funcionalidad avanzada. En este capítulo analizaremos algunas ideas acerca de estos importantes componentes de los SIG en la actualidad y veremos las principales alternativas existentes, al tiempo que estudiaremos los fundamentos de bases de datos necesarios para comprender la forma en que los datos espaciales se almacenan en las bases de datos actuales. Asimismo, y para entender la situación presente y conocer las ventajas e inconvenientes de los distintos métodos de almacenar la información en los SIG, veremos la evolución de estos respecto a la arquitectura de almacenamiento de información.
MODELO RELACIONAL
1: Modelo relacional: modelo de organización y gestión de bases de datos consistente en el almacenamiento de datos en tablas compuestas por filas, o tuplas, y columnas o campos. Se distingue de otros modelos, como el jerárquico, por ser más comprensible para el usuario inexperto, y por basarse en la lógica de predicados para establecer relaciones entre distintos datos. Surge como solución a la creciente variedad de los datos que integran las data warehouses y podemos resumir el concepto como una colección de tablas (relaciones).
2: El modelo relacional, para el modelado y la gestión de bases de datos, es un modelo de datos basado en la lógica de predicados y en la teoría de conjuntos. Tras ser postuladas sus bases en 1970 por Edgar Frank Codd, de los laboratorios IBM en San José (California), no tardó en consolidarse como un nuevo paradigma en los modelos de base de datos. Su idea fundamental es el uso de relaciones. Estas relaciones podrían considerarse en forma lógica como conjuntos de datos llamados tuplas. Pese a que esta es la teoría de las bases de datos relacionales creadas por Codd, la mayoría de las veces se conceptualiza de una manera más fácil de imaginar, pensando en cada relación como si fuese una tabla que está compuesta por registros (cada fila de la tabla sería un registro o "tupla") y columnas (también llamadas "campos"). Es el modelo más utilizado en la actualidad para modelar problemas reales y administrar datos dinámicamente.

TUPLA:
1: Una tupla es una secuencia de valores agrupados.
Una tupla sirve para agrupar, como si fueran un único valor, varios valores que, por su naturaleza, deben ir juntos.
El tipo de datos que representa a las tuplas se llama tuple. El tipo tuple es inmutable: una tupla no puede ser modificada una vez que ha sido creada.
Una tupla puede ser creada poniendo los valores separados por comas y entre paréntesis. Por ejemplo, podemos crear una tupla que tenga el nombre y el apellido de una persona:
>>> persona = ('Perico', 'Los Palotes')>>> persona('Perico', 'Los Palotes')
2:En matemáticas, una tupla es una lista ordenada de elementos. Una n-tupla es una secuencia (o lista ordenada) de n elementos, siendo n un número natural (entero no-negativo). La única 0-tupla es la secuencia vacía. Una n-tupla se define inductivamente desde la construcción de un par ordenado. Las tuplas suelen anotarse listando sus elementos entre paréntesis " ", separados por comas. Por ejemplo,
", separados por comas. Por ejemplo,  denota una 5-tupla. En ocasiones se usan otros delimitadores, como los corchetes "
denota una 5-tupla. En ocasiones se usan otros delimitadores, como los corchetes "![{\displaystyle [{\text{ }}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f5f326cf9d5d53f32fe85b216202414ed697927) " o las angulares "
" o las angulares " ". Las tuplas suelen emplearse para describir otros objetos matemáticos, como los vectores. Esto es, una lista con un número limitado de objetos (una secuencia infinita se denomina en matemática como una familia, aunque hay autores que consideran el término tupla para denominar no solo listas finitas). Las tuplas se emplean para describir objetos matemáticos que tienen estructura; es decir, que son capaces de ser descompuestos en un cierto número de componentes. Por ejemplo, un grafo dirigido se puede definir como una tupla de (V, E), donde V es el conjunto de nodos y E es el subconjunto de V × V que denota las aristas del grafo.
". Las tuplas suelen emplearse para describir otros objetos matemáticos, como los vectores. Esto es, una lista con un número limitado de objetos (una secuencia infinita se denomina en matemática como una familia, aunque hay autores que consideran el término tupla para denominar no solo listas finitas). Las tuplas se emplean para describir objetos matemáticos que tienen estructura; es decir, que son capaces de ser descompuestos en un cierto número de componentes. Por ejemplo, un grafo dirigido se puede definir como una tupla de (V, E), donde V es el conjunto de nodos y E es el subconjunto de V × V que denota las aristas del grafo.
 ", separados por comas. Por ejemplo,
", separados por comas. Por ejemplo,  denota una 5-tupla. En ocasiones se usan otros delimitadores, como los corchetes "
denota una 5-tupla. En ocasiones se usan otros delimitadores, como los corchetes "![{\displaystyle [{\text{ }}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f5f326cf9d5d53f32fe85b216202414ed697927) " o las angulares "
" o las angulares " ". Las tuplas suelen emplearse para describir otros objetos matemáticos, como los vectores. Esto es, una lista con un número limitado de objetos (una secuencia infinita se denomina en matemática como una familia, aunque hay autores que consideran el término tupla para denominar no solo listas finitas). Las tuplas se emplean para describir objetos matemáticos que tienen estructura; es decir, que son capaces de ser descompuestos en un cierto número de componentes. Por ejemplo, un grafo dirigido se puede definir como una tupla de (V, E), donde V es el conjunto de nodos y E es el subconjunto de V × V que denota las aristas del grafo.
". Las tuplas suelen emplearse para describir otros objetos matemáticos, como los vectores. Esto es, una lista con un número limitado de objetos (una secuencia infinita se denomina en matemática como una familia, aunque hay autores que consideran el término tupla para denominar no solo listas finitas). Las tuplas se emplean para describir objetos matemáticos que tienen estructura; es decir, que son capaces de ser descompuestos en un cierto número de componentes. Por ejemplo, un grafo dirigido se puede definir como una tupla de (V, E), donde V es el conjunto de nodos y E es el subconjunto de V × V que denota las aristas del grafo.
3:En las ciencias de la computación una tupla puede tener dos significados distintos. Generalmente en los lenguajes de programación funcional y en otros lenguajes de programación, una tupla es un objeto que bien puede tener datos o diversos objetos, de forma similar a una tupla definida matemáticamente. Un objeto de este tipo es conocido también como record.
ATRIBUTO:
1: En informática, un atributo es una especificación que define una propiedad de un objeto, elemento o archivo. También puede referirse o establecer el valor específico para una instancia determinada de los mismos.
Sin embargo, actualmente, el término atributo puede y con frecuencia se considera como si fuera una propiedad dependiendo de la tecnología que se use.
Para mayor claridad, los atributos deben ser considerados más correctamente como metadatos. Un atributo es con frecuencia y en general una característica de una propiedad.
Un buen ejemplo es el proceso de asignación de valores XML a las propiedades (elementos). Tenga en cuenta que el valor del elemento se encuentra antes de la etiqueta de cierre (por separado), no en el propio elemento. El mismo elemento puede tener una serie de atributos establecidos (Nombre = "estoesunapropiedad").
Si el elemento en cuestión puede ser considerado una propiedad (Nombre_Cliente) de otra entidad (digamos "cliente"), el elemento puede tener cero o más atributos (propiedades) de su propio (Nombre_Cliente es de Tipo = "tipotexto").
2:Atributo. Los atributos son las características individuales que diferencian un objeto de otro y determinan su apariencia, estado u otras cualidades. Los atributos se guardan en variables denominadas de instancia, y cada objeto particular puede tener valores distintos para estas variables. Las variables de instancia también denominados miembros dato, son declaradas en la clase pero sus valores son fijados y cambiados en el objeto. Además de las variables de instancia hay variables de clase, las cuales se aplican a la clase y a todas sus instancias.
DOMINIO
1:En matemáticas, el dominio (conjunto de definición o conjunto de partida) de una función  es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien
o bien  . En
. En  se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío. Por otra parte, el conjunto de todos los resultados posibles de una función dada se denomina codominio de esa función.
se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío. Por otra parte, el conjunto de todos los resultados posibles de una función dada se denomina codominio de esa función.
 es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien
o bien  . En
. En  se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío. Por otra parte, el conjunto de todos los resultados posibles de una función dada se denomina codominio de esa función.
se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío. Por otra parte, el conjunto de todos los resultados posibles de una función dada se denomina codominio de esa función.
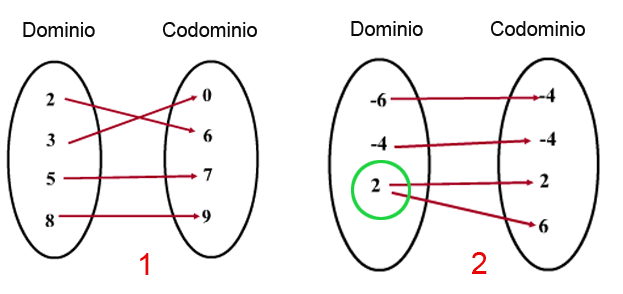
2:Del latín dominĭum, el dominio es la facultad o la capacidad que dispone una persona para controlar a otras o para hacer uso de lo propio. El concepto puede asociarse a la potestad o a la autoridad.
REGLAS DEL MODELO RELACIONAL DE Codd
- Regla 0: Regla de fundación Cualquier sistema que se proclame como relacional, debe ser capaz de gestionar sus bases de datos enteramente mediante sus capacidades relacionales.
- Regla 1: Regla de la información. Toda la información en la base de datos es representada unidireccionalmente por valores en posiciones de las columnas dentro de filas de tablas. Toda la información en una base de datos relacional se representa explícitamente en el nivel Lógico exactamente de una manera: con valores en tablas.
- Regla 2: Regla del acceso garantizado. Todos los datos deben ser accesibles sin ambigüedad. Esta regla es esencialmente una nueva exposición del requisito fundamental para las llaves primarias. Dice que cada valor escalar individual en la base de datos debe ser lógicamente direccionable especificando el nombre de la tabla, la columna que lo contiene y la llave primaria.
- Regla 3: Regla del tratamiento sistemático de valores nulos. El sistema de gestión de base de datos debe permitir que haya campos nulos. Debe tener una representación de la "información que falta y de la información inaplicable" que sea sistemática y distinta de todos los valores regulares.
- Regla 4: Catálogo dinámico en línea basado en el modelo relacional. El sistema debe soportar un catálogo en línea, el catálogo relacional, que da acceso a la estructura de la base de datos y que debe ser accesible a los usuarios autorizados.
- Regla 5: Regla comprensiva del sublenguaje de los datos. El sistema debe soportar por lo menos un lenguaje relacional que:
- Tenga una sintaxis lineal.
- Puede ser utilizado de manera interactiva.
- Tenga soporte de operaciones de definición de datos, operaciones de manipulación de datos (actualización así como la recuperación), de control de la seguridad e integridad y operaciones de administración de transacciones.
- Regla 6: Regla de actualización de vistas. Todas las vistas que son teóricamente actualizables deben poder ser actualizadas por el sistema.
- Regla 7: Alto nivel de inserción, actualización y borrado. El sistema debe permitir la manipulación de alto nivel en los datos, es decir, sobre conjuntos de tuplas. Esto significa que los datos no solo se pueden recuperar de una base de datos relacional a partir de filas múltiples y/o de tablas múltiples, sino que también pueden realizarse inserciones, actualización y borrados sobre varias tuplas y/o tablas al mismo tiempo y no sólo sobre registros individuales.
- Regla 8: Independencia física de los datos. Los programas de aplicación y actividades del terminal permanecen inalterados a nivel lógico aunque realicen cambios en las representaciones de almacenamiento o métodos de acceso.
- Regla 9: Independencia lógica de los datos. Cualquier cambio a nivel físico que preserve la información deberá mantener los programas de aplicación y las actividades de la terminal intactos. La independencia de datos lógica es más difícil de lograr que la independencia física de datos.
- Regla 10: Independencia de la integridad. Las restricciones de integridad se deben especificar por separado de los programas de aplicación y almacenarse en la base de datos. Debe ser posible cambiar esas restricciones sin afectar innecesariamente a las aplicaciones existentes.
- Regla 11: Independencia de la distribución. La distribución de porciones de base de datos en distintas localizaciones debe ser invisible a los usuarios de la base de datos. Los usos existentes deben continuar funcionando con éxito:
- cuando una versión distribuida del SGBD se carga por primera vez
- cuando los datos existentes se redistribuyen en el sistema.
- Regla 12: La regla de la no subversión. Si el sistema proporciona una interfaz de bajo nivel de registro, aparte de una interfaz relacional, esa interfaz de bajo nivel no debe permitir su utilización para subvertir el sistema. Por ejemplo para sortear las reglas de seguridad relacional o las restricciones de integridad. Esto es debido a sistemas no relacionales previamente existentes se les añadió una interfaz relacional pero, al mantener la interfaz nativa, seguía existiendo la posibilidad de trabajar no relacionalmente.





















 .
.

